8 - Добавяне на графичен примитив

Честит втори сняг!

В тази статия ще добавим нова фигура (графичен примитив). Това може да се наложи да направите на изпита. Затова е добре, след като приключите всичко друго по програмата да добавите една нова фигура за тренировка.

Добавяне на фигура

Новият графичен примитив ще бъде малко по-сложен - петолъчка.

Започваме с добавянето на бутон за петолъчка, по същия начин, както добавяхме превключващи бутони в статия 2 - Графичен интерфейс.

 Задаваме групата на бутона.

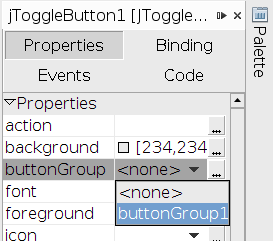
Променяме името му на „jToggleButtonPentagram“.

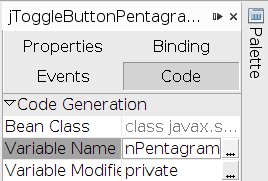
Вместо да пишем изцяло нов клас „MyPentagram“ ще използваме наготово „MyEllipse“, като ще променим само каквото е нужно от него.

Копираме класа „MyEllipse“ и го поставяме с рефакторинг в пакета „trayangle“.

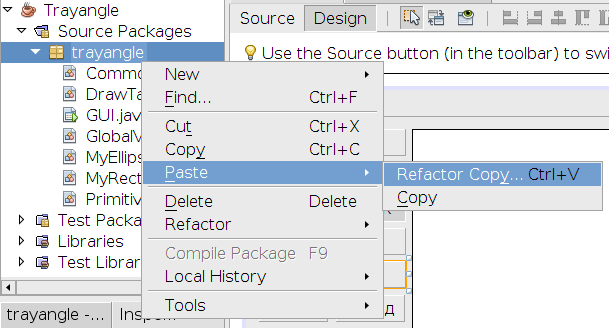
Променяме името му на „MyPentagram“.

Нека оставим за накрая промяната на кода в „MyPentagram“. Ако не го променим въобще вместо да се рисува петолъчка ще се рисува елипса.

Преди това трябва да променим другия код в програмата така, че да работи с новата фигура.

За да не пропуснем нещо можем да открием всички места, на които се използва класът, на някоя от нашите работещи фигури. Нека това да е елипсата. Щракваме с десния бутон върху името на класа и търсим всички негови срещания в кода.

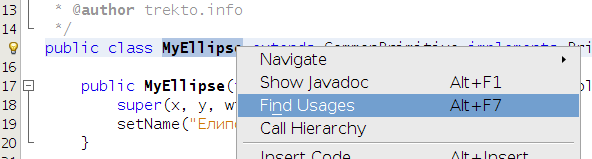
NetBeans открива, че класът „MyEllipse“ се използва само на две места.

Хмм. Щом са само две това означава, че дизайнът на програмата не е толкова лош и може би няма чак толкова да навреди на вашето развитие, като софтуерни разработчици :) Все пак има някои лоши практики в него.

Първото място е в метода „jPanelCanvasMouseDragged“. Добавяме още един „else if“ блок, почти същия, като този за елипсата, но вече използваме новите бутон и клас - тези за петолъчката.

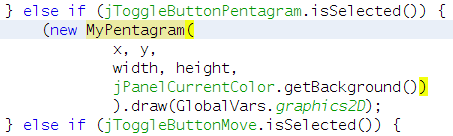
Същото правим и на второто място - в метода „jPanelCanvasMouseReleased“.

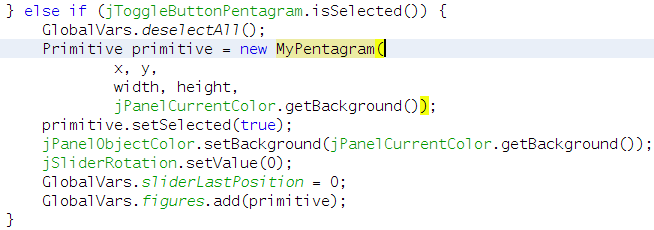
Чудесно!

Нека променим и класа „MyPentagram“.
Сменяме името, което се изписва в графичния списък с фигури, да е „Петолъчка“.

Остава да променим единствено метода „draw“ така, че той да рисува петолъчка.

Това ще е най-трудната част, защото трябва да измислим по какъв начин ще нарисуваме сложната фигура.

В класа „Graphics“ няма метод, който директно да рисува петолъчка. Ще трябва ние да я нарисуваме точка по точка използвайки метода „fillPolygon“.

Единият вариант на този метод приема като параметър обект от тип „Polygon“, а той от своя страна представлява затворена област в двуизмерната равнина. Тази област се описва от множество от точки, които са свързани помежду си. Например, за да опишем правоъгълник можем да ползвам точките с координати (10, 10), (90, 10), (90, 60), (10, 60) в тази последователност.

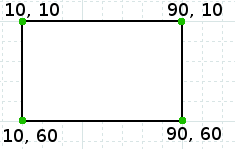
При създаването на петолъчка трябва да изчисляваме точките, които я описват, като вземаме предвид къде ще се намира и с какви широчина и височина трябва да бъде.

Нека първо неформално дефинираме геометричната фигура петолъчка. Ще го направим описвайки как може да я начертаем.

Правим окръжност. Разделяме я на 5 равни дъги. Те трябва да са с мярка по 72 градуса, защото 360 / 5 = 72. Всяка от петте точки разделящи окръжността свързваме с нейните две срещуположни (по-отдалечените) точки. Фигурата получена от свързващите отсечки се нарича петолъчка (пентаграм на английски).

 

Формална дефиниция може да откриете в Wikipedia: Пентаграм.

Забележете, че не всяка звезда с пет лъча е петолъчка, например тази:

За да нарисуваме петолъчка ще подходим по начина използван в програмата демонстрираща използването на OpenGL в C++.

В нея се рисува приближение на окръжност изградено от 360 на брой свързани последователно точки. За да намерим координатите на тези точки използваме отношенията между страните в правоъгълен триъгълник (тригонометрия).

Когато знаем радиуса и координатите на центъра на една окръжност можем лесно да намерим координатите на всяка точка от окръжността.

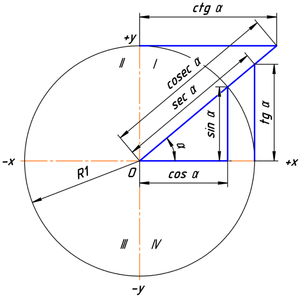
Ако центърът ѝ съвпада с центъра на координатната система, то пресечната точка на права сключваща ъгъл α с абсцисната ос, с окръжността в I-ви квадрант е (точката) с координати x = cos(α) * r и y = sin(α) * r, където r  е радиусът на окръжността.

Ако r е различно при пресмятането на x и y, ще се получи точка от елипса, а не от окръжност.

Петолъчката ще бъде изградена от общо 5 * 2 на брой последователно свързани точки. 5 точки за върховете на лъчите и 5 точки, в които се пресичат образуващите отсечки. За да намерим координатите на точките, в които се пресичат отсечките ни е достатъчно да знаем разстоянието от тях до центъра на петолъчката (нека го наречем вътрешен радиус на петолъчката). Като си припомним и малко геометрия пресмятаме, че той е R * cos(α) / cos(α / 2), където R е разстоянието от центъра до връх на лъч (или външен радиус), а α е ъгълът между отсечките свързващи центъра с върховете на два съседни лъча. Той както казахме по-горе е 72 градуса.

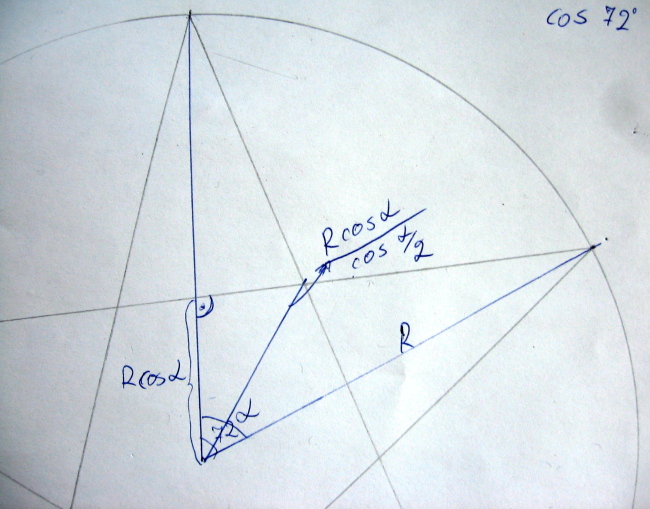
Вероятно тези от вас, които разбират малко от тригонометрия вече са наясно с написаното по-горе, а тези, които не разбират продължават да не си разбират, но трябваше да опитам :)

Вече можем да пристъпим към кода.

Най-напред правим някои инициализации.

Външните радиуси за „x“ и „y“ определяме от широчината и височината на правоъгълната област, в която ще се намира петолъчката. Вътрешните намираме, както описахме преди малко.

Добре ще изглежда ако един от лъчите на петолъчката сочи право нагоре, затова трябва да я нагласим, като започваме да въртим цикъла не от 0, а от начален ъгъл 90 - 72 = 18 градуса.

Стъпката на цикъла е 72 / 2 = 36 градуса. В него най-напред проверяваме дали сме стигнали до точка от лъч или до точка на пресичане на образуващи отсечки. Това става като от текущия ъгъл извадим началния и ако разликата е кратна на 72 значи сме до точка на пресичане и ще изчисляваме координатите ѝ използвайки вътрешния радиус. В противен случай сме до връх на лъч и използваме външния радиус.

Важно е да отбележим, че ъглите в класа „Graphics“ се измерват по часовниковата стрелка, а не както сме свикнали от математиката обратно на часовниковата стрелка. Така например ъгъл с мярка 18 градуса ще се намира в IV-ти квадрант.

Накрая в цикъла добавяме точката към полигона, като към координатите ѝ добавяме координатите на цялата фигура - „x“ и „y“.

С „fillPolygon“ рисуваме областта определена от добавените точки и сме готови.

Така нарисувана петолъчката „не запълва“ цялата маркирана област.

Това се получава, защото ние изчисляваме радиусите, като разделим широчината и височината на 2. По този начин само лъчите, които са перпендикулярни на някоя от страните на маркираната област ще я допират. В случая това е само горният лъч.

Използвайки малко геометрия може да поправите това. Аз ще го оставя така, защото е задоволителен вариант и защото иначе кодът ще стане още повече.

Оказа се, че методът „draw“ е доста сложен или поне е сложно да се обясни :)

Все пак на изпита може да се наложи да нарисувате фигура и трябва да можете да пресметнете какви ще са нейните координати.

Друг вариант, вместо да се ползва обект от тип „Polygon“, е да създадете сложна фигура използвайки няколко по-прости. Например може да нарисувате нещо като звезда използвайки два квадрата завъртяни на 45 градуса един спрямо друг.

Допълнение при избор на цвят

Докато създавах изображението в края на тази страница забелязах, че ако щракнем на „Cancel“ или просто затворим прозореца за избор на цвят, текущият такъв се променя. Добре би било в този случай да си остава същия.

Аналогично на това, което направихме с прозорците за избор на файл трябва да проверяваме дали диалоговият прозорец връща обект от тип „Color“ или връща „null“.

Също така вместо да подаваме началния цвят по подразбиране, до сега сме подавали зеления: „Color.GREEN“.

Ето как изглежда кодът за избор на текущ цвят след тази промяна.

И кодът за избор цвят на обект.

Създаване на изпълнима програма

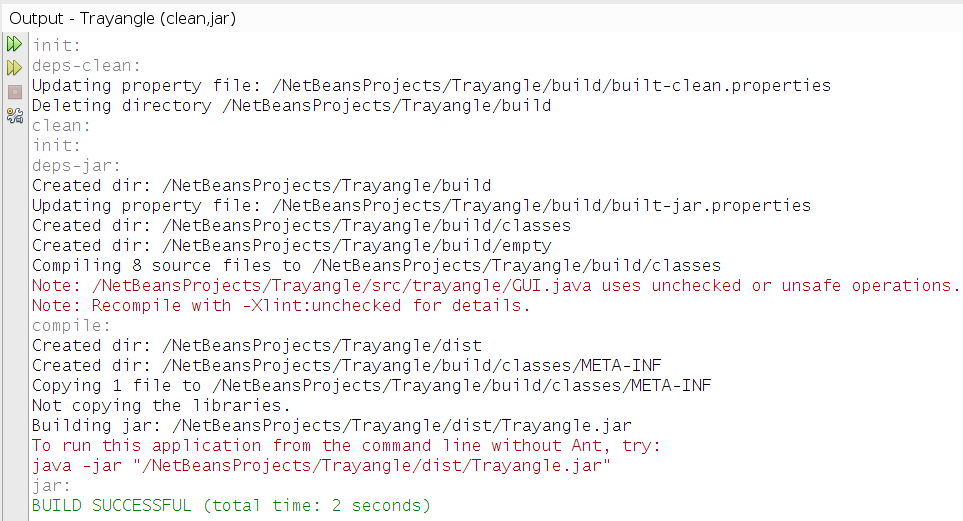
За да създадем изпълнима (от виртуалната машина на Java) програма можем да щракнем на бутона „Изчисти и създай“ („Clean and Build“).

В прозореца „Output“ NetBeans ни извежда съобщения свързани със създаването на програмата, както и с коя команда да я стартираме.

И така, ето го последния изглед на програмата ни (поне за тази година).

Това е целият NetBeans проект - Trayangle-NetBeans-project.zip. Разбира се в него се съдържа изходният код.

Програмата - Trayangle-8.jar

Картинката - Slunchogledi_vecher.trn

<< 7 - Допълнителни функции

Заключение >>