Някои проблеми могат да се разбият на по-малки подпроблеми. Ако успеем да решим подпроблемите можем да решим и главния проблем. Подпроблемите от своя страна също могат да се представят, като подпроблеми и така, докато се стигне до такива, които се директно решими. Когато тези подпроблеми се припокриват се налага да решаваме някои от тях по повече от един път.

Нека да вземем за пример числата на Фибоначи: 0, 1, 1, 2, 3, 5, 8, 13... По дефиниция първото и второто число са 0 и 1, a Fib(n) = Fib(n-1) + Fib(n-2) т.е. за да намерим n-тото число трябва да знаем предишните две. Fib(n-1) и Fib(n-2) са два по-малки подпроблема, които трябва да бъдат решени за да намерим Fib(n). Тъй като самата дефиниция е рекурсивна, веднага можем да напишем рекурсивна функция, намираща n-тото число:

int fib(int n) {
	if(n == 1) return 0;
	if(n == 2) return 1;
	return fib(n-1) + fib(n-2);
}

Примерно, за да намерим Fib(6) трябва да намерим Fib(5) и Fib(4). От своя страна, за да намерим Fib(5) трябва да намерим Fib(4) и Fib(3)... Това се вижда от следното изображение:

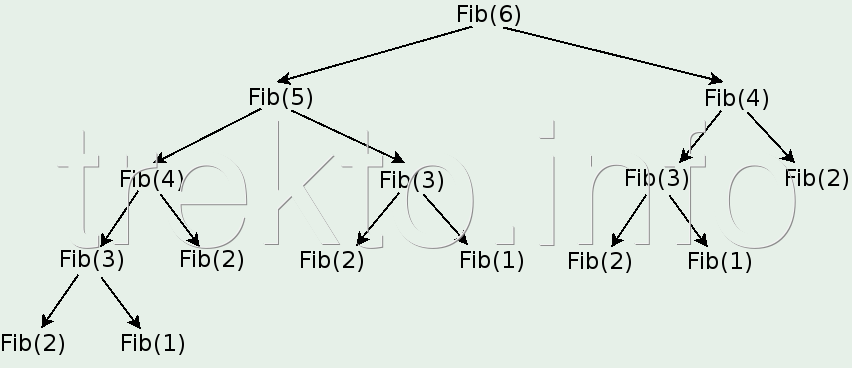
Функциите се извикват съответно:
	Fib(4) - 2 пъти
	Fib(3) - 3 пъти.
	Fib(2) - 5 пъти
	Fib(1) - 3 пъти

При динамичното оптимиране, известно още и като динамично програмиране се ползва на готово (информацията за) решението на даден проблем, без да се решава отново. Това може да доведе до многократно ускорение.

За да подобрим горната рекурсивна функция ще ползваме масив (в общия случай асоциативен т.е. map), в който ще пазим изчислените вече стойности. На позиция i ще поставяме i-тото число на Фибоначи. Преди да изчислим наново едно число ще проверим дали вече не е било изчислено. Първоначално масивът трябва да е занулен.

int fib(int n) {
	if(n == 1) return 0;
	if(n == 2) return 1;
	if(!map[n]) map[n] = fib(n-1) + fib(n-2);	// ако не е пресметнато го пресмятаме и запазваме
	return map[n];					// връщаме вече пресметнатото число
}

Този подход се нарича отгоре-надолу, защото започваме да решаваме проблема от върха (погледнете изображението по-горе).
При подхода отдолу-нагоре първо се изчисляват fib(1) и fib(2) и се използват, за да се изчисли fib(3), fib(4) и т.н.:

int fib(int n) {
	if(n == 1) return 0;
	if(n == 2) return 1;
	int prevFib = 0, currFib = 1;
	for(int i = 0; i < n-2; i++) {
		int newFib = prevFib + currFib;		// изчисляваме новото число използвайки предишните две
		prevFib = currFib;
		currFib = newFib;
	}
	return currFib;
}

В последния вариант на функцията се използва памет само за 3 променливи.

Друг пример за динамично оптимиране е търсенето на най-пряк път между два върха в граф.

За да намерим най-прекия път от 1 до 10 можем да намерим най-преките пътища от съседите на 1 (върхове 2 и 3) до 10. Тогава ще имаме 2 възможности за пътя от 1 до 10: през връх 2 и през връх 3.
Дължината на пътя през връх 2 е равна на дължината на реброто (1, 2) + дължината на намерения най-пряк път от 2 до 10.
Дължината на пътя през връх 3 е равна на дължината на реброто (1, 3) + дължината на намерения най-пряк път от 3 до 10.
Остава просто да сравним кой от тези два пътя е по-кратък.
За да намерим най-прекия път от 2 до 10 и от 3 до 10 прилагаме същия алгоритъм. Правим това и за най-прекия път от 4 до 10 и т.н. докато стигнем до върхове 7 и 9, които са пряко свързани с 10 и дължината на пътя е равна на дължината на ребрата.

Така описания рекурсивен подход ще изчисли дължината на пътя между 4 и 10 два пъти, а тази между 8 и 10 четири пъти. За да избегнем това можем да съхраняваме вече изчислената дължина на пътя между два върха в таблица, в която на ред i, позиция j ще се намира дължината на пътя между върховете i и j. Когато се наложи да ползваме стойността, просто я вземаме от таблицата вместо да я изчисляваме отново.

Подобна идея е заложена в алгоритъма на Белман-Форд за намиране на най-пряк между два върха в граф.

Повече за динамичното оптимиране може да научите от Wikipedia.

За да демонстрираме връщането назад (backtracking) ще направим алгоритъм, който решава играта судоку.

Най-простият възможен начин за решаването ѝ е чрез използването на „груба сила“ (brute force). Ще генерираме всички възможни разположения на цифрите и за всяка от тях ще проверяваме дали е решение. За горния пример, където имаме 46 празни позиции и на всяка от тях можем да поставим една от 9-те цифри, възможните разположения ще бъдат 9⁴⁶, което е необозримо много.

Трябва да измислим алгоритъм, който по време на генерирането на едно разположение да проверява дали то ще доведе до решение и ако установи, че няма, да прекратява генерирането и да преминава към следващото разположение. Това представлява връщането назад - изоставяме текущия път, по който сме тръгнали (защото в далечината виждаме, че води към пропаст) и се връщаме назад, за да поемем по друг път. За разлика от него „грубата сила“ стига чак до края на пътя, установява, че има пропаст и тогава продължава със следващия възможен път.

Ето един алгоритъм с връщане назад:

Прилагайки го за горното судоку започваме от позиция [1, 1] и установяваме, че там можем да разположим цифри 1, 2 или 5. Поставяме 1 и продължаваме с позиция [1, 2], където можем да поставим единствено 7. Сега за позиция [1, 3] можем да поставим 2, 5 или 8. Ако поставим 2 то на позиция [1, 4] можем да сложим единствено 8, но тогава на позиция [1, 5] не може да поставим никоя цифра. Тук правим връщане назад, за да изберем втората възможност за позиция [1, 3] - 5. Всичко това се вижда ясно от дървото на решенията:

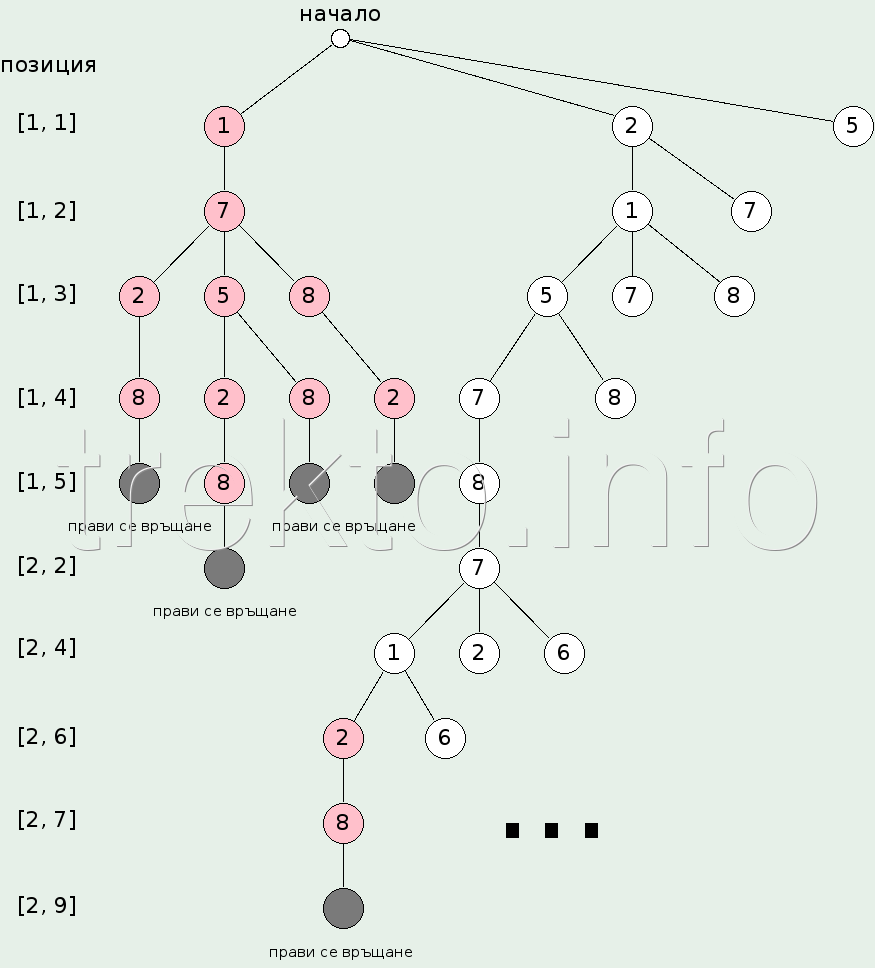
Горният алгоритъм е реализиран в програмата sudoku.cpp. Тя ползва файла stopwatch.h за да засече времето за изпълнение. Като входен параметър се задава името на файла, който съдържа играта. За тази по-горе ползвайте файла sudoku.txt. В него на първия ред се задава размерът на полето. Програмата работи с размер на полето 9 и 4. Може да я свалите за мобилния си телефон от тук: судоку за мобилен телефон.

За да разберете по-лесно кода ползвайте файла sudoku_light.cpp, който е олекотена версия на sudoku.cpp и работи само за размер 9x9. В него не се извършват проверки за коректността на входните данни, не се засича времето за изпълнение, както и броят направени връщания.

Решението на горната задача изглежда така:

Ако искаме да намерим всички възможни решения на дадена игра, трябва след като сме намерили първото, вместо да прекратим търсенето, да направим връщане назад и така докато повече не можем да правим връщане. С други думи: обхожда се дървото на решенията. Това също е реализирано в sudoku.cpp.

Алгоритъмът предложен тук не е особено умен. Опитайте се да го подобрите, като по някакъв начин по-рано установите, че избраният път не води до решение и трябва да се направи връщане.

За разлика от судоку, за една от най-старите игри - Го не е известен алгоритъм, който днешните изчислителни машини могат да изпълнят за разумно кратко време, поради огромния брой възможни комбинации.

Освен за backtracking може да прочетете и за backjumping.

Ето анимации показващи нагледно връщането назад.

А тук е показано как се решава дадена судоку игра стъпка по стъпка.

Главна страница

<< Упражнение 8 - Графи

Упражнение 10 - Контролна 2 >>