Двоичното търсене в подреден масив е много ефективно и се извършва по следния начин:
Сравняваме дали търсеният елемент е равен на средния елемент. Ако е равен - Край.
Ако търсеният е по-малък от средния продължаваме търсенето в левия подмасив.
Ако търсеният е по-голям от средния продължаваме търсенето в десния подмасив.
Сравняваме дали търсеният е равен на средния елемент на подмасива. Ако е равен - Край.
Ако търсеният е по-малък от средния продължаваме търсенето в левия подмасив на подмасива.
Ако търсеният е по-голям от средния продължаваме търсенето в десния подмасив на подмасива.
...
Ако подмасивът стане с дължина 1 и това не е търсеният елемент значи го няма.

За да приложим двоично търсене за динамична структура от данни ще използваме дърво за двоично търсене. Но първо нека въведем някои неформални определения.

Структурата от данни дърво е изградена от свързани йерархично възли (елементи):

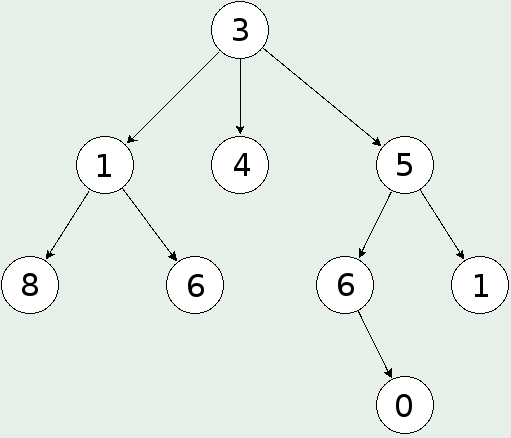
Възлите могат да имат 0 или повече връзки към други възли. Първите се наричат родители, а вторите наследници или деца. Възелът без родител се нарича корен. Всеки друг възел има точно по един родител. Възлите без наследници се наричат листа или терминални възли. Връзките между възлите още се наричат ребра. Ако приемем, че дължината на всички ребра е равна на единица то дълбочина на възел наричаме дължината на пътя от възела до корена. Множеството от възли с еднаква дълбочина се обозначава, като ниво. Коренът е на ниво 0. В дървото по-горе, възлите 1, 4 и 5 са на ниво 1. Височина на дървото ще наричаме най-дългия път от корена до листо + 1. Така височината на дървото по-горе е 4. Тегло на дървото е броят на възлите му. Теглото на горното дърво е 9.

За формално определение и още дефиниции, може да погледнете дървото в Wikipedia.

Пирамидата (heap) е дърво, в което стойността на всеки родител е по-голяма или равна от стойностите на неговите наследници. Двоично дърво е дърво, на което всеки възел има не повече от 2 наследника, наричани ляв и десен наследник.

Дърво за двоично търсене е такова двоично дърво, на което всички възли в лявото поддърво са по-малки от корена, а всички възли в дясното поддърво са по-големи от него. Лявото и дясното поддърво от своя страна също трябва да са дървета за двоично търсене.
Всъщност ако в дървото съхраняваме не числа, а възли от произволен тип, то всички те трябва да имат уникални ключове, по който да ги сравняваме.
Дърво за двоично търсене:

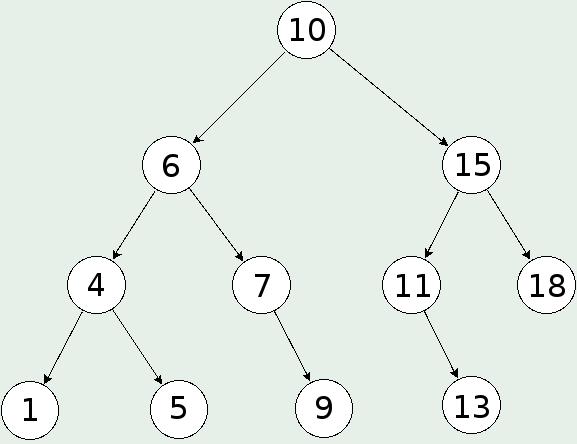
Ще разгледаме по-подробно дървото за двоично търсене. Възлите му в C++ ще представяме, като структура с 3 полета. Първото ще са данните, като в примерите самите данни ще са и ключът. Второто ще е указател към левия наследник, а третото - указател към десния наследник. Ако възелът няма наследници указателите му ще сочат към NULL. В класа Дърво ще имаме поле от тип указател към възел, което ще сочи към корена на дървото или към NULL ако дървото е празно.

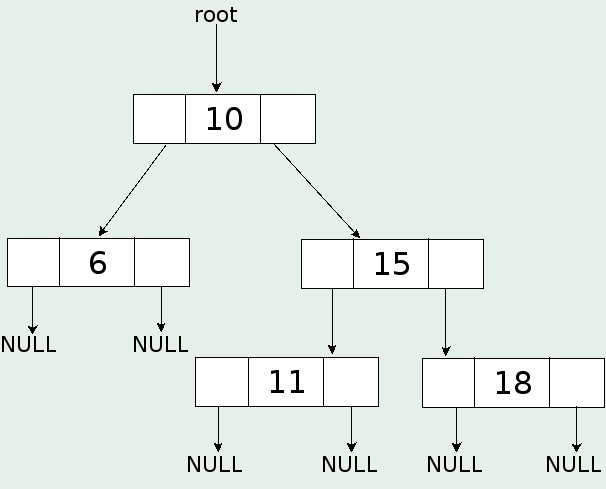
Някои автори дефинират указателя към корена да е на ниво 0, а самият корен да е на ниво 1.

Операциите, които ще извършваме с дървото за двоично търсене, освен самото търсене разбира се, са добавяне и премахване на възли. Също така трябва да изтрием цялото дърво, когато свършим работата си с него.

Търсенето в такова дърво става по следния начин:
Правим текущ възел коренът.
Докато текущият възел е различен от NULL:
Ако текущият възел е търсеният - Край.
Ако търсеният е по-малък от текущия, текущ става левият наследник.
В противен случай текущ става десният наследник.
Ако сме стигнали до тук, значи търсеният възел го няма в дървото.

Използвайки този алгоритъм, за да намерим даден възел или да установим, че го няма е нужно да извършим най-много h на брой сравнения, където h е височината на дървото. Ето защо търсенето в това дърво е толкова ефективно.

При добавянето на нов възел трябва да се запазва свойството всички възли в лявото поддърво да са по-малки от корена и всички възли в дясното поддърво да са по-големи от него. Новият възел ще се появи като листо, но трябва да намерим къде точно. Това става започвайки от корена и слизайки надолу към листата. Ако възелът, който трябва да добавим е по-малък от текущия продължаваме спускането по левия клон, а в противен случай по десния.

Изтриването на цялото дърво можем да извършим по следния начин:
Ако указателят към корена сочи към NULL - Край.
Изтриваме лявото поддърво използвайки текущия алгоритъм.
Изтриваме дясното поддърво използвайки текущия алгоритъм.
Изтриваме текущия възел и насочваме указателя, към него, към NULL.

Изтриването на само един възел е по-трудно от изтриването на цялото дърво, защото след това дървото трябва да продължи да бъде дърво за двоично търсене.
Ако възелът, който ще изтриваме няма наследници - просто го изтриваме.
Ако има само един наследник - насочваме указателя сочещ към възела, към наследника му и изтриваме възела.
Ако има два наследника тогава всъщност няма да изтриваме самия възел, а някой от неговите наследници. Стойността на наследника ще копираме във възела, който искаме да изтрием. За да се запази свойството на дървото трябва да направим това с най-големия възел, по-малък от този, който искаме да изтрием или най-малкия, по-голям от него. Нека изберем първия вариант - да намерим най-големия възел в лявото поддърво. За да постигнем това е нужно да тръгнем по лявото поддърво и в него да вървим все надясно, докато стигнем възел, който няма десен наследник. Нека наречем този възел temp. След това копираме неговата стойност във възела, който искаме да изтрием и изтриваме temp. Той (temp) или няма наследници или има ляв наследник, а тези случаи вече описахме по-горе.

Обхождането на дървото може да стане по 3 различни начина:
Инфиксно (LVR): най-напред обхождаме лявото поддърво, после възела, след това дясното;
Префиксно (VLR): най-напред обхождаме възела, после лявото поддърво, след това дясното;
Постфиксно (LRV): най-напред обхождаме лявото поддърво, после дясното, след това възела.

За да отпечатаме възлите на дървото в нарастващ ред трябва да го обходим инфиксно:
Отпечатваме цялото ляво поддърво;
Отпечатваме корена;
Отпечатваме цялото дясно поддърво.

Във файла bst.cpp е реализиран класът Дърво, деклариран по-долу. В метода findPointer е изнесен код, общ за няколко други метода. За да разберете какво точно правят методите findPointer и deleteNode си припомнете указателите и псевдонимите. Трябва да ги разбирате добре, за да разберете как работят тези методи. Декларация на класа Дърво:

template <class T>
struct Node {						// структура Възел
	T data;						// стойност или ключ на възела
	Node* left;					// указател към левия му наследник
	Node* right;					// указател към десния му наследник
};

template <class T>
class Tree {						// клас Дърво
private:
	Node<T>* root;					// указател към корена на дървото
	void copyTree(Node<T>* srcRoot, Node<T>* &dstRoot);	// копира дървото с корен srcRoot
								// в дървото с корен dstRoot
	void deleteTree(Node<T>* &aRoot);		// изтрива дървото с корен aRoot
	Node<T>* &findPointer(const T &aData);		// връща псевдоним на указателя към мястото
							// в дървото, където трябва да се намира aData
	void printTree(Node<T>* aRoot) const;		// отпечатва дървото с корен aRoot

public:
	Tree();						// конструктор по подразбиране
	Tree(const Tree &aTree);			// копиращ конструктор
	~Tree();					// деструктор
	void addNode(T aData);				// добавя възел
	void deleteNode(const T &aData);		// изтрива възела със стойност aData
	Node<T>* find(const T &aData);			// връща указател към възела със стойност aData
	void print() const;				// отпечатва дървото
	Tree<T> &operator = (const Tree &aTree);	// оператор за присвояване
};

Забележете, че редът на добавяне на възлите в дървото оказва влияние на неговата балансираност. Ако възлите, които добавяме са предварително сортирани ще се получи следната ситуация:

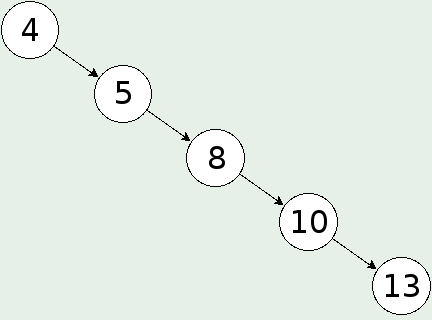
Това дърво не прилича много на дърво за двоично търсене, въпреки, че е такова. За такива дървета казваме, че са небалансирани.

Двоично дърво с балансирана височина, AVL дърво или просто балансирано дърво е такова, което притежава свойството за всеки възел височините на лявото и дясното му поддърво да се различават най-много с единица.
Двоично дърво с балансирана височина:

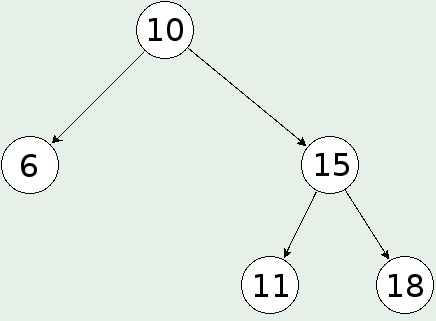
Идеално балансирано двоично дърво е такова, на което всеки възел има ляво и дясно поддърво, в които броят на възлите (теглата) се различава най-много с единица:

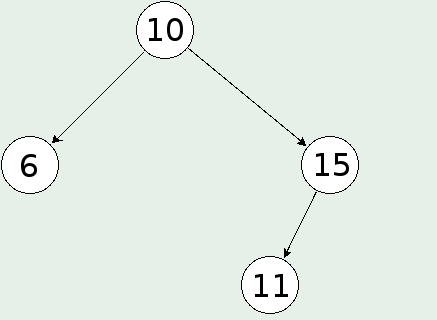
Съществуват още доста видове дървета. Едни от тях са B-дърветата, които понякога се бъркат с двоичните дървета. B-дърветата всъщност са обобщение на дърветата за двоично търсене, защото възлите им могат да имат повече от два наследника. Друг вид са префиксните дървета (trie) и червено-черните дървета.

Главна страница

<< Упражнение 6 - Контролна

Упражнение 8 - Графи >>